This article appears in the March 2019 edition of the Microwave Journal.
David W. Porterfield, Jr, Ph.D., Micro Harmonics Corporation
Introduction
Isolators are non-reciprocal devices, passing EM signals in one direction and absorbing them in the reverse direction. They are primarily used to suppress standing waves that arise due to impedance mismatches between highly-tuned components such as those found in frequency multiplier chains. The standing waves cause dips or even nulls in the output of the multiplier chain. They can be mitigated by inserting isolators between the multipliers resulting in a much smoother frequency response and improved bandwidth.
Traditional Faraday rotation isolators provide more than 20 dB isolation over full waveguide bands, with some exceeding 30 dB. There are over a dozen vendors worldwide, but the design has largely remained static since the 1970’s. Insertion loss is low in the microwave bands, but steadily increases with frequency. At mm-wave (MMW) frequencies the insertion loss becomes problematic. In the WR‑10 band (75-110 GHz) the insertion loss can exceed 3 dB. In the WR-3.4 band (220-330 GHz) the insertion loss can be more than 7 dB, making them impractical. There are few vendors in the bands above 110 GHz. Isolators in the WR-4.3 and WR-3.4 bands were produced many years ago but are now difficult to find. At these frequencies the constituent parts are very small, and difficult to fabricate and align. And with more than 7 dB insertion loss, there isn’t much demand.
In 2001, Erickson [1] demonstrated that the insertion loss can be dramatically reduced. But for many years following that work, very little had changed in the commercial market. In 2015, with funding from NASA JPL, Micro Harmonics Corporation developed a line of MMW isolators designed for low insertion loss. These new isolators have a typical insertion loss of less than 1 dB at WR-10 and about 2 dB at WR-3.4. These numbers are game changers and MMW system developers are now reconsidering their use. Micro Harmonics is currently the only worldwide producer of full waveguide band, low-loss isolators in the WR-4.3 (170-260 GHz) and WR-3.4 (220-330 GHz) bands. We are aiming even higher to the WR-2.8 (265-400 GHz) and WR-2.2 (330-500 GHz) bands.
Faraday Rotation Isolator Theory
At frequencies from 50-330 GHz, the dominant isolator topology is Faraday rotation with transitions to rectangular waveguide as described by Barnes [2] in 1961. At the heart of the isolator are a cylindrical ferrite core and a pair of alumina cones bisected on their central axes by resistive layers. The cones couple the dominant TE10 waveguide mode to the HE11 hybrid dielectric mode in the ferrite. The ferrite and cones are suspended in the waveguide structure by a pair of washer shaped supports. The output cone and waveguide are rotated 45° with respect to the input cone and waveguide. An absorber is used to suppress higher order modes near the ferrite core.
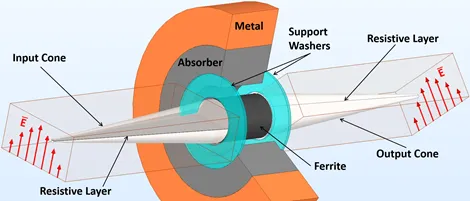 |
| Figure 1 – Functional sketch of a Faraday rotation isolator. |
The sketch in Figure 1 shows some of the functional parts. For improved visibility in the sketch, the absorber is split in half and the top half of the input cone is semi-transparent. The E-field in the TE10 mode is normal to the resistive layer in the input waveguide. The field is rotated 45° CCW as it passes through the ferrite and emerges normal to the resistive layer in the output cone. No currents are generated in either resistive layer by the forward travelling wave and there is no associated loss. The direction of rotation is the same for both the forward and reverse waves giving rise to the non-reciprocal nature of the device. The reverse travelling wave is rotated into the input cone resistive layer and absorbed (converted to heat energy).
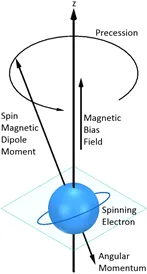 |
| Figure 2 – Angular momentum and spin magnetic dipole moment vectors. |
All materials have electron spin states that give rise to magnetic dipoles. In non-magnetic materials the dipoles are randomly aligned and there is no net magnetic dipole moment. In ferrite materials some of the magnetic dipole moments can be aligned. Application of a DC magnetic bias field causes additional dipoles to align and the magnetic moment increases. Further increases in the magnetic bias field give rise to larger net magnetic dipole moments until a point of saturation is reached, beyond which further increases in the bias field produce no change. This condition is referred to as magnetic saturation. The magnitude of the saturation magnetization (4πMs) is a material dependent property and varies in the range 300-5000 gauss for most commercial ferrites. The magnetic dipoles precess around the magnetic bias field vector as shown in the graphic in Figure 2. As an EM signal passes through the ferrite, the fields interact with the dipole moments. Linearly polarized waves, like those passing through the isolator, can be decomposed into left hand (LHCP) and right hand (RHCP) circularly polarized waves. The interaction with the precessing dipole moments gives rise to disparate propagation constants for the RHCP and LHCP waves. The difference in the propagation constants arises because one of the components (RHCP or LHCP) opposes the dipole precession and the other coincides. A phase shift occurs between the RHCP and LHCP waves as they travel through the ferrite. This gives rise to the rotation of the linearly polarized signal. A more in-depth discussion on Faraday rotation is given by Pozar [3], Lax et. al [4] and Balanis [5].
Simulations
At Micro Harmonics, we use HFSS [6] to model and simulate isolator performance. The final models contain all relevant parts including the core region surrounding the ferrite, the waveguides and twist steps. The simulations include the Faraday rotation effect using a magnetically biased ferrite. The graph in Figure 3 shows simulation data (dashed lines) and measured data (solid lines) for a Micro Harmonics WR-5.1 isolator. The HFSS model includes waveguide conductor losses as well as ferrite dielectric loss.
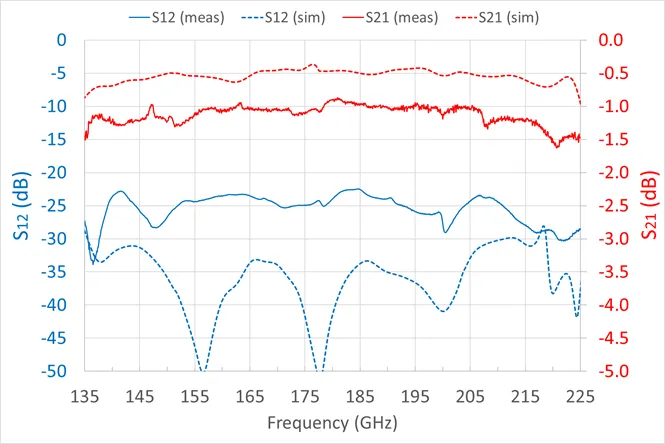 |
| Figure 3 – Measured and simulation data for a WR-5.1 isolator. |
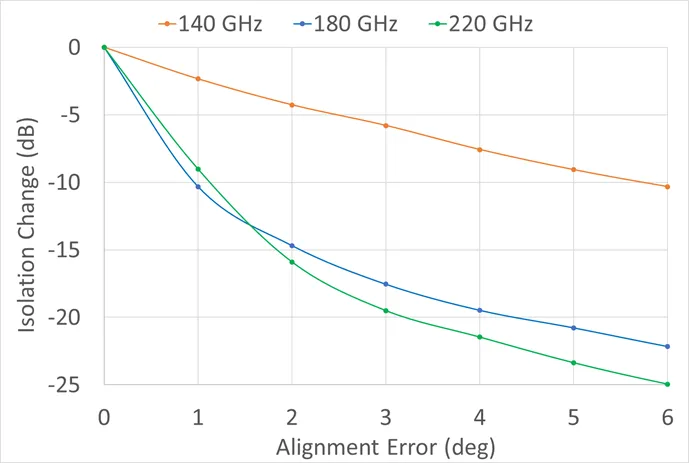 |
| Figure 4 – Change in isolation caused by a rotational misalignment of the input cone. |
The simulated insertion loss is about 0.5 dB lower than the measured data. The discrepancy is likely due to small misalignments in the assemblies and under-estimation of the waveguide conductor loss in the models. There is very little data on material parameters at these frequencies which contributes to inaccuracy in the models. The measured data compares favorably to old-style isolators with insertion loss greater than 4 dB in this band. The discrepancy in the simulated and measured isolation data (-S12) can also be attributed to small alignment errors and fabrication errors in the constituent parts. Qualitatively the data are in good agreement. The standard WR-5.1 band is 140-220 GHz. The data are shown over an extended band from 135-225 GHz.
To illustrate the sensitivity to alignment and fabrication errors we ran a series of HFSS simulations on our WR-5.1 isolator model. In the simulations the input cone was incrementally rotated out of alignment while every other part was held in perfect alignment. The data are shown in the graph in Figure 4. The isolation is degraded by 10 dB for a 1° alignment error at the center and upper end of the WR-5.1 band. A fabrication error of only ± 0.001 inch in the ferrite length also causes a 1° rotational error with similar results.
There are challenges fabricating and assembling MMW isolators. The constituent parts are tiny and as we just illustrated, even small alignment errors can significantly degrade performance. Misalignment can cause increased coupling to higher order modes in the region near the ferrite core resulting in unwanted structure in the response. The assembly process is an art form and no two isolators have the same signature. We continually strive to improve the uniformity of our assemblies. We also test every isolator on a vector network analyzer to ensure conformity with specifications.
Minimizing Insertion Loss
Two of the largest contributing factors to insertion loss at MMW frequencies are 1) loss in the ferrite and 2) waveguide conductor loss. A good starting point is to consider the equation for EM field rotation in a Faraday rotation isolator.
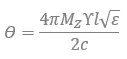 |
Where,
- 4πMZ is the axial magnetization
- ϒ is the gyromagnetic ratio (8.795×106xg rad/s/Oe)
- l is the ferrite length
- c is the speed of light
- ? is the ferrite dielectric constant
This equation shows that the field rotation is directly proportional to the ferrite length and the axial magnetization. Minimum insertion loss and maximum isolation occur when the EM field is rotated by 45° as it passes through the ferrite. Ferrites are lossy at MMW frequencies, so it is essential that the length be reduced as much as possible. The traditional method used to tune Faraday rotation isolators is to use ferrites that are substantially longer than the minimum required length and adjust the magnetic bias field to achieve precise 45° rotation. This is a useful way to tune the isolator, but it comes at the cost of increased insertion loss. The insertion loss is greater because 1) the ferrite is longer and 2) unsaturated ferrites have higher loss per unit length [3, 7]. In this precisely tuned state, the isolators are sensitive to stray magnetic fields which can cause under- or over-rotation of the signal. A ferromagnetic sheath is typically employed to channel stray magnetic fields away from the ferrite. But even with a sheath in place there is some sensitivity.
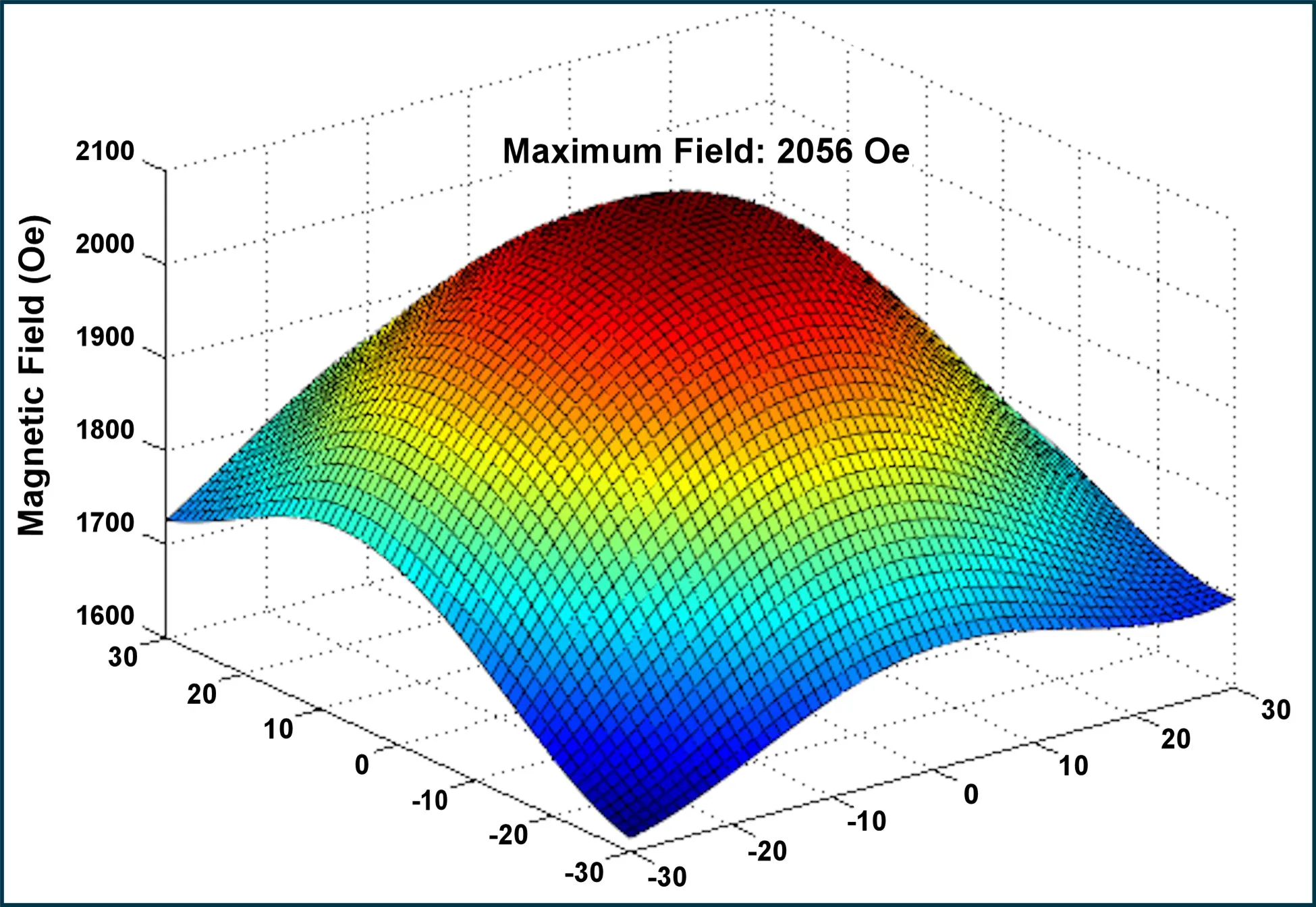 |
| Figure 5 – Measured magnetic bias field near the surface of the ferrite. |
At Micro Harmonics, we use a saturating magnetic bias field and the minimum possible ferrite length. This yields the absolute minimum loss in the ferrite core. The magnetic bias fields are measured to ensure ferrite saturation. Magnetic armatures are used to achieve a focused, uniform bias field in the ferrite. The graph in Figure 5 shows the measured magnetic bias field near the surface of the ferrite. The peak measured value of 2000 Oe is substantially more than what is required for saturation. Only stray magnetic fields with a very strong axial component in the opposite polarity can impact signal rotation.
2) Minimizing Waveguide Loss
Because the EM field is rotated by 45° as it passes through the ferrite, it is necessary to realign the flanges. Traditionally this is accomplished by twisting extruded waveguide as shown in the photo in Figure 6. The twist is implemented over a sufficiently long distance to avoid damaging the extruded guide. In the WR-10 through WR-3.4 bands the total length of extruded waveguide is typically more than 2 inches. At Micro Harmonics we replace the extruded twist with machined twist steps that are substantially shorter and yield good broadband performance and reduced waveguide loss. The total flange-to-flange length of a Micro Harmonics WR-3.4 isolator is only 0.45 inch. At WR-10 the reduction in waveguide loss is only 0.2 dB, but at WR-3.4 the reduction is close to 1 dB.
 |
| Figure 6 – Traditional style Faraday rotation isolator with extruded twist. |
Pushing to Higher Bands
 |
|---|
| Figure 7 – Cored alumina cylinder with resistive layer. |
One of the biggest challenges at the higher frequencies is fabrication of the alumina cones. The traditional method to produce the cones begins by laminating two alumina plates together with a resistive layer at the interface. The plates are turned on their side and cored, producing alumina cylinders with a resistive layer bisecting the central axis as shown in Figure 7. The cylinders are ground to a cone shape. It is difficult to get tip diameters less than 0.004 inch. Few machinists can fabricate the cones for our WR-4.3 and WR-3.4 isolators. The problem becomes even greater at WR-2.8 and WR-2.2.
 |
|---|
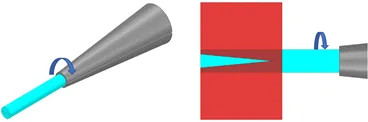
| Figure 8 – (Left) Chucked alumina cylinder. (Right) Rotating cylinder during cold laser ablation (red area denotes exposure to laser). |
We are experimenting with alternative techniques to form the smallest cones. Cold laser ablation is an appealing approach because 1) no pressure is applied to the alumina, 2) there is no heating which can lead to damage of the epoxy and resistive layers, and 3) it may be possible to form cones with very small tips. The cored cylinders have two ends that are flat and orthogonal to the central axis and suitable for use as cone bases. The alumina cylinder is chucked and rotated as shown in the sketch in Figure 8. As the material is ablated, the cone eventually detaches from the cylinder.
Diamond Heatsinks
In most commercial Faraday rotation isolators, the ferrite and cones are suspended by a pair of washer-shaped supports as shown in Figure 1. The cone & ferrite assembly is inserted through the inner support holes and then attached with a non-conductive epoxy. The support material is typically BOPET, Styrene, a resin or some other material with a low dielectric constant and low loss at MMW frequencies. Materials with these characteristics are generally in the class of thermal insulators and thus the cones and ferrite are thermally isolated from the metal block.
 |
|---|
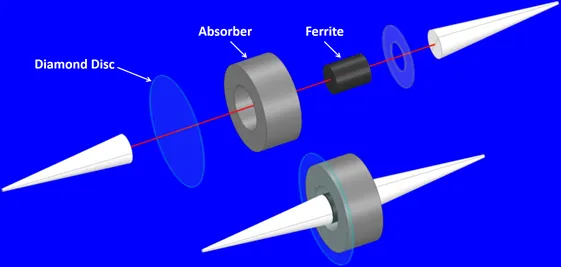
| Figure 9 – Exploded view of the core assembly. |
| . |
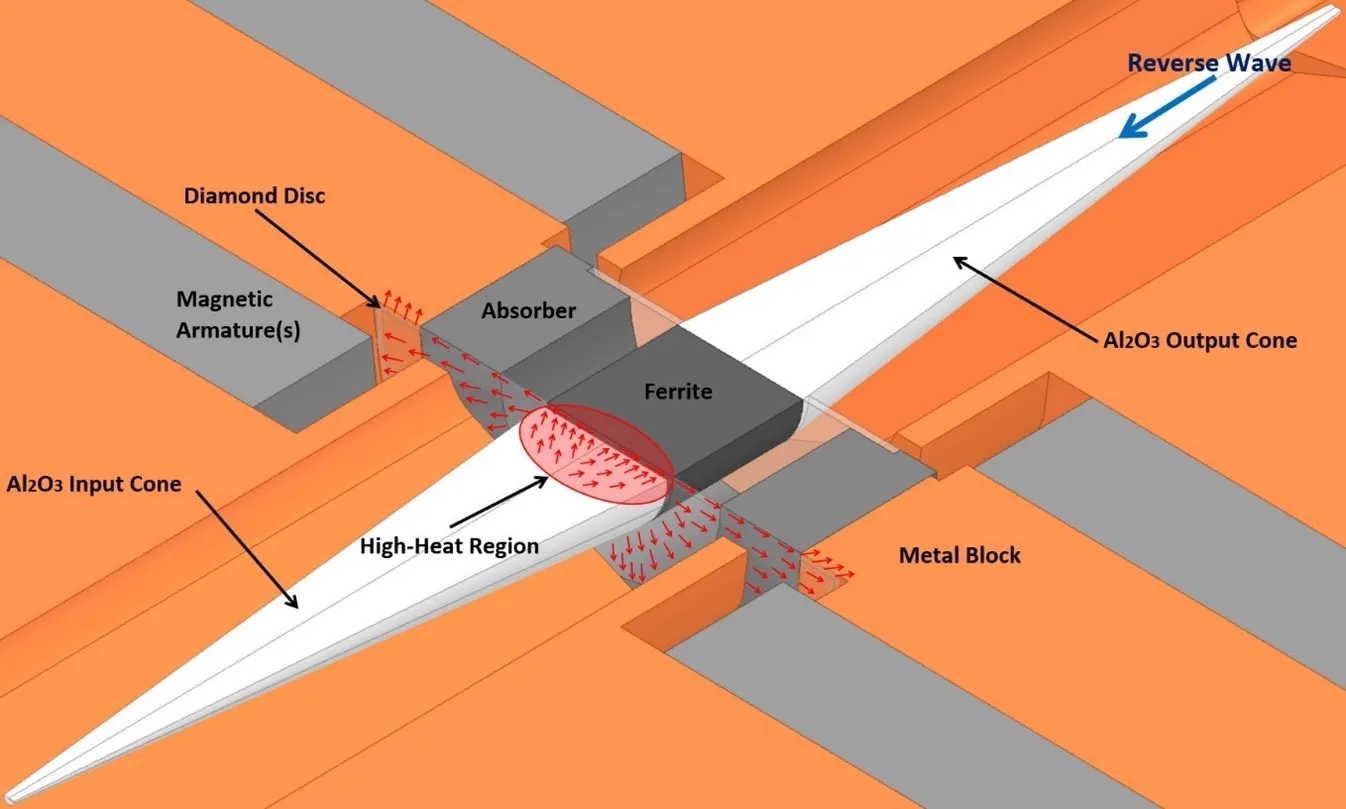 |
| Figure 10 – Sketch showing the path of heat dissipation through the diamond. |
Absorbed power from the reverse travelling wave is converted to heat energy in the input cone. Very little of this heat energy can be channeled away by thermal conduction through the washer-shaped supports, rather it must be dissipated through a radiative process or by means of convection through the surrounding air. The resistive layers are thus subject to high heat levels and even damage if too much reverse power is incident on the device. As higher power sources are becoming available there is a renewed interest in the power ratings of these devices.
At Micro Harmonics we replace the input support washer with a uniform high-grade optical CVD diamond disc as shown in Figure 9. The thermal conductivity of diamond is near 2200 W/mK, more than five times higher than copper. The diamond disc is sandwiched between the base of the input cone and the ferrite and is in intimate contact over the entire area of the cone base. This is the optimal location for the diamond disc since it is the region subject to the highest heat levels.
As illustrated in the graphic in Figure 10, the diamond disc is attached to the metal waveguide block over its entire periphery and thus provides an excellent conduit to channel heat away from the resistive layer. The red arrows indicate the path of heat flow. This topology is clearly superior for thermal conduction. These isolators should handle higher reverse power levels while maintaining lower core temperatures for improved reliability.
Cryogenic Applications
NASA recently awarded Micro Harmonics a contract to develop a line of isolators optimized for use at cryogenic temperatures. Aside from issues with thermal stress there is also a substantial temperature dependence of the ferrite saturation magnetization. The measured isolation of our WR-10 isolator drops from 30 dB at 290 K to 14 dB at 77 K. The degradation is caused by a 10° over-rotation of the EM fields arising from the higher magnetization at 77 K. Ferrite magnetization follows a modified Bloch Law;
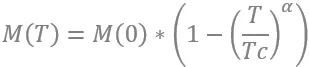 |
Where,
- M(T) = Magnetization
- Tc = Curie temperature
- M(0) = Magnetization at 0 K
- α = Temperature exponent
 |
|---|
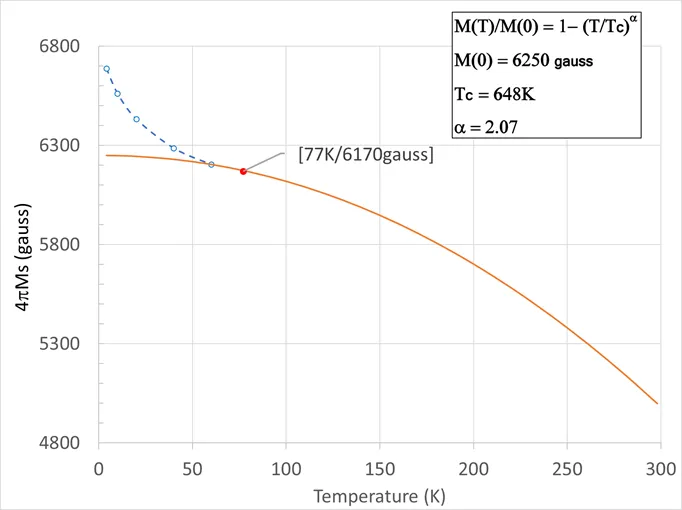
| Figure 11 – Temperature dependence of the saturation magnetization. |
The Bloch Law typically follows an α = 3/2 form [8], but there is evidence in the literature to suggest that a modified Bloch Law with α =2 is a better fit to the data for nickel spinel ferrites [9, 10]. The decrease in magnetization at high temperatures is due to the increasing excitation of spin waves which makes it more difficult to align the magnetic dipoles. The Curie temperature (Tc), is the temperature at which materials lose their permanent magnetic properties.
We fit our measured data to a modified Bloch Law using M(77 K) = 6170 gauss, Tc = 648 K, M(0 K) = 6250 gauss and α =2.07. The curve is plotted in red in Figure 11. There is some evidence in the literature that the magnetization can depart from the modified Bloch law at temperatures below 50 K (blue curve) depending on ferrite particle size [10].
Conclusion
A new and innovative line of MMW isolators covering every waveguide band from WR-15 through WR-3.4 (50-330 GHz) is now available from Micro Harmonics Corporation. These isolators employ diamond heatsinks for improved thermal conduction. Typical insertion loss is less than 1 dB at WR-10 (75-110 GHz) and less than 2 dB at WR-3.4 (220-330 GHz). This is a dramatic improvement over the previous state-of-the-art. Isolators at WR-2.8 (265-400 GHz) and WR-2.2 (330-500 GHz) are under development and tentatively scheduled for release sometime in 2020. A separate line of MMW isolators designed for use in cryogenic systems is also currently under development with the first bands scheduled for release in the Fall of 2019.
Acknowledgements
We would like to thank NASA for their continued support of this work through research contracts NNX15CP37P, NNX16CP07C and 80NSSC18P2018.
References
[1] N. R. Erickson, “Very Low Loss Wideband Isolators for mm-Wavelengths,” 2001 IEEE MTT-S Dig., pp. 1175-1178.
[2] C.E. Barnes, “Broad-band Isolators and Variable Attenuators for Millimeter Wavelengths,” IEEE Trans. Microw. Theory Tech., vol. 9, pp. 519-523, 1961.
[3] David Pozar, “Microwave Engineering,” Wiley.
[4] Benjamin Lax and Kenneth Button, “Microwave Ferrites and Ferrimagnetics,” McGraw Hill
[5] Constantine Balanis, “Advanced Engineering Electromagnetics,” Wiley; 2 ed, 2012.
[6] High Frequency Structure Simulator (HFSS), 3D EM simulation, Ansys Corporation.
[7] Naima Ghoutia Sabri , “Nonreciprocal Propagation in Ferrite Medium and Their Applications – Microwave Circulator,” Int. Jrnl. of Comp. Sci. and Elec. Eng. (IJCSEE) Vol 1, Is 2 (2013) ISSN 2320–4028.
[8] Charles Kittel, “Introduction to Solid State Physics”, Wiley.
[9] R.N. Bhowmik, K.S. Aneeshkumar, “Low temperature ferromagnetic properties, magnetic field induced spin order and random spin freezing effect in Ni1.5Fe1.5O4 ferrite,” Department of Physics, Pondicherry University, India.
[10] K. Maaz, A. Mumtaz, S.K. Hasanain, M.F. Bertino, “Temperature dependent coercivity and magnetization of nickel ferrite nanoparticles,” Jrnl. of Mag. and Mag. Mat., 322, 2010, pp. 2199–2202.
